1．プログラムの特色

本プログラムでは、社会から求められている「数学的な考え方を用いて、問題点を整理し解決する力」を身につけることができます。具体的には1、2年次に数学の基礎を固め、3年次からはそれぞれの興味に応じた専門科目を選択し学びます。専門科目は解析学、代数学、幾何学、応用数学から自由に選ぶことができます。特定の分野を中心に深く学ぶことも、また数学の理論からその応用までを幅広く身につけることも可能です。

2．2年次の教育カリキュラム内容

このように数学はあらゆる科学の基礎を支える最も重要な基幹学問の1つです。そして数学的なものの考え方は様々な場面において大変有用であることも分かっています。現代のように種々の問題が絡み合い複雑化した社会では、それを解決するための基礎として数学・応用数学の重要性が高まる一方です。21世紀においても数学・応用数学は重要な学問として益々発展していくでしょう。

3．3年次の教育カリキュラム内容

上述の基礎科目の内容をさらに押し進め、より専門的な数学を学びます。解析学・代数学・幾何学・応用数学の各分野において複数の科目が開講されます。これらの専門科目の中から自由に科目を選択し、それぞれの興味に応じた分野を学修します。特定の分野の科目を集中的に深く学ぶこともできますし、複数の分野の科目を広く学ぶことも可能です。さらに数学を主体として応用数学までの幅広い分野の知識を修得することもできます。

4．4年次の教育カリキュラム内容

最終学年では、これまで修得した知識をもとに、それぞれが選んだ研究室において専門分野の学修をセミナー形式で行います。セミナーでは、これまでの受け身の講義とは異なり、自分で本を読み参考文献を調べ、内容を理解し、理解した事柄を他者に正確に伝えることを学びます。内容の十分な理解はもちろん、他者に理解させるための発表の仕方や質問に対する適切な対応などのプレゼンテーション能力とコミュニケーション能力を養います。

5．履修の流れ

2年次2学期に配属プログラムが確定します。解析学、代数・幾何学、集合と位相の他に微分方程式やプログラミングも選択することができます。3年次には解析学・代数学・幾何学・応用数学の各分野において複数の専門科目が開講されます。これらの科目からより専門的な内容を学びます。4年次にはセミナー形式の学修により、専門分野をさらに深く修得します。

6．授業紹介---科目の内容紹介---

複素解析学
   これまでに学んできた微分積分学をさらに発展させ、複素数を変数とする複素数値関数の微分積分を学ぶ科目です。変数が複素数になることで、実数の場合では想像もできなかった世界が広がっていることを知ります。 その一例がよく知られているオイラーの公式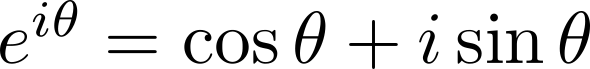です。複素関数の世界を知ることにより、実数の世界がより鮮明に観えてきます。

7．就職状況

中学校・高等学校数学教員、公務員、システム・ソフトウェア開発、銀行、証券、保険、自動車、鉄道、不動産、建築などの多種多様な企業への就職実績があります。大学院に進学し、数学をさらに深く学ぶことも可能です。

詳しくはこちら